Handwritten Digits Prediction using Neural Networks

Working of neural networks to predict handwritten digits is shown in this blog.
ML
Coding
Author

Kishan Ved

Published

August 9, 2023

#Neural Network for predicting handwritten digits

Generating data

from keras.datasets import mnist

(X_train, y_train), (X_test, y_test)= digits = mnist.load_data()
print(X_train.shape)
print(X_test.shape)
(60000, 28, 28)
(10000, 28, 28)

Changing 3D arrays to 2D arrays

import numpy as np
X_train = np.array([X_train[i].ravel() for i in range(X_train.shape[0])])
X_train.shape
(60000, 784)
X_test = np.array([X_test[i].ravel() for i in range(X_test.shape[0])])
X_test.shape
(10000, 784)

Defining the model

import tensorflow as tf
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
model = Sequential([
    Dense(units=25,activation='relu'),
    Dense(units=15,activation='relu'),
    Dense(units=10,activation='linear')
])
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
              optimizer = tf.optimizers.Adam(0.00001),)

Fitting data into our model

model.fit(X_train,y_train,epochs=50)
Epoch 1/50
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0796
Epoch 2/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0722
Epoch 3/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0697
Epoch 4/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0682
Epoch 5/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0671
Epoch 6/50
1875/1875 [==============================] - 5s 2ms/step - loss: 0.0662
Epoch 7/50
1875/1875 [==============================] - 5s 2ms/step - loss: 0.0654
Epoch 8/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0648
Epoch 9/50
1875/1875 [==============================] - 5s 2ms/step - loss: 0.0642
Epoch 10/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0637
Epoch 11/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0632
Epoch 12/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0628
Epoch 13/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0625
Epoch 14/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0621
Epoch 15/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0618
Epoch 16/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0615
Epoch 17/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0613
Epoch 18/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0610
Epoch 19/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0607
Epoch 20/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0605
Epoch 21/50
1875/1875 [==============================] - 8s 4ms/step - loss: 0.0603
Epoch 22/50
1875/1875 [==============================] - 7s 3ms/step - loss: 0.0601
Epoch 23/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0598
Epoch 24/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0597
Epoch 25/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0595
Epoch 26/50
1875/1875 [==============================] - 6s 3ms/step - loss: 0.0592
Epoch 27/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0591
Epoch 28/50
1875/1875 [==============================] - 5s 2ms/step - loss: 0.0589
Epoch 29/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0588
Epoch 30/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0586
Epoch 31/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0584
Epoch 32/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0582
Epoch 33/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0581
Epoch 34/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0580
Epoch 35/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0578
Epoch 36/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0577
Epoch 37/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0576
Epoch 38/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0574
Epoch 39/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0572
Epoch 40/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0571
Epoch 41/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0570
Epoch 42/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0569
Epoch 43/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0567
Epoch 44/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0565
Epoch 45/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0564
Epoch 46/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0563
Epoch 47/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0562
Epoch 48/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0561
Epoch 49/50
1875/1875 [==============================] - 5s 3ms/step - loss: 0.0560
Epoch 50/50
1875/1875 [==============================] - 4s 2ms/step - loss: 0.0558
<keras.callbacks.History at 0x7da45a7ac430>

Model’s predictions

z = model.predict(X_test)
z
313/313 [==============================] - 1s 1ms/step
array([[  72.16857  ,  141.73775  ,   96.48515  , ...,  154.52151  ,
         121.25679  ,  132.14868  ],
       [  -0.627826 ,   -3.3008962,    5.777237 , ...,   -2.4945285,
           0.6228762,    0.7712919],
       [-230.27592  ,  258.76544  ,   64.82611  , ..., -130.3381   ,
         -27.08746  , -234.17287  ],
       ...,
       [  34.202644 ,   43.17494  ,   33.014576 , ...,   53.978813 ,
          40.810585 ,   55.017437 ],
       [ 138.34541  ,  144.58145  ,   81.53359  , ...,  156.82513  ,
         158.51685  ,  143.86653  ],
       [ 116.74089  ,  120.48703  ,   86.29796  , ...,   48.32769  ,
         111.52056  ,   98.84621  ]], dtype=float32)

Converting predicted values to digits

pred = np.array([np.argmax(z[i]) for i in range(len(z))])
pred
array([7, 2, 1, ..., 4, 5, 6])
print(pred.shape)
print(y_test.shape)
(10000,)
(10000,)

Accuracy of our Neural Network

from sklearn.metrics import accuracy_score
accuracy_score(y_test,pred)*100
95.38
from sklearn.metrics import confusion_matrix
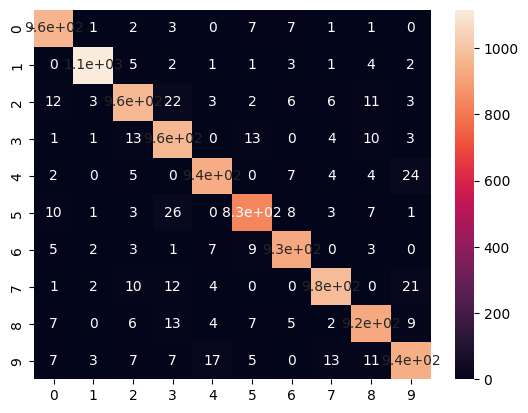
import seaborn as sns
cf = confusion_matrix(y_test,pred)
sns.heatmap(cf,annot=True)
<Axes: >