Matrix Transformations

Understanding matrix multiplication as transformation and interpretation of low rank matrices
ML
Math
Coding
Author

Kishan Ved

Published

July 20, 2023

Matrix Multiplication as Transformation and Interpretation of Low Rank Matrices

Matrix multiplication as transformation

When a vector is multiplied by a suitable matrix, the operation essentially transforms the original vector into a new vector. This can be illustrated by the following example. The dimension of the resultant vector may also change (though it does not in this example).

Necessary imports:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import seaborn as sns
from sympy import Eq,Matrix,MatMul

Creating a vector and a transformation matrix

A = np.array([[2,1],[1,4]])
x = np.array([1,1])
Ax = A @ x
Eq(Matrix(Ax),MatMul(Matrix(A),Matrix(x)),evaluate=False)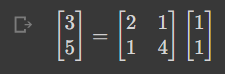

A function to plot arrows

def plot_arrow(ax,v,color,label):
    arrow = mpatches.FancyArrowPatch((0,0),(v[0],v[1]),mutation_scale=9,color=color,label=label)
    ax.add_patch(arrow)
    ax.legend(bbox_to_anchor=(1.6,1),borderaxespad=0)

A function to compute the transformed vector

def plot_transform(A,x):
  Ax = A @ x
  fig, ax = plt.subplots()
  plot_arrow(ax,x,"k",f"Original Vector x: {x}")
  plot_arrow(ax,Ax,"g",f"Transformed vector Ax: {Ax}")
  plt.xlim((-5,5))
  plt.ylim((-5,5))
  plt.grid(alpha=0.1)
  ax.set_aspect("equal")

Using the above functions

plot_transform(np.array([[2.0,1.0],[1.0,4.0]]),np.array([1.0,1.0]))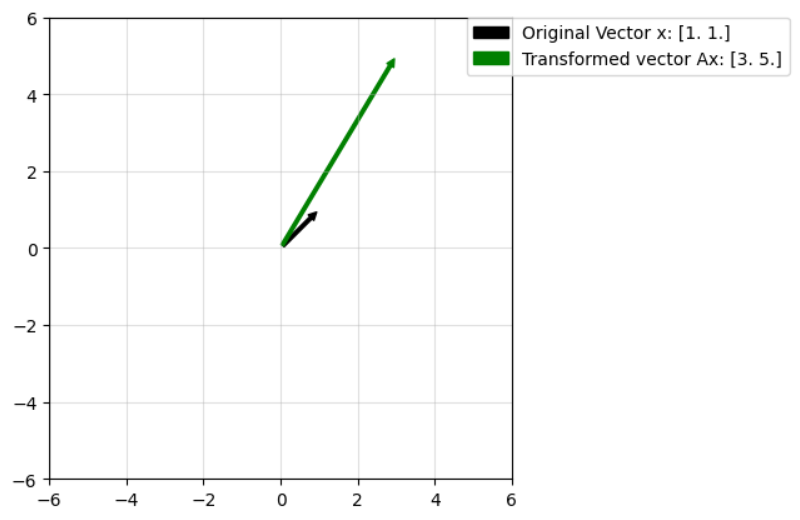

Using matrix transformation to rotate a vector

Defining the required function

def plot_rot(theta,v):
  c = np.cos(theta)
  s = np.sin(theta)
  rot_mat = np.array([[c,-s],[s,c]])
  w = rot_mat @ v
  fig, ax = plt.subplots()
  plot_arrow(ax,v,"k",f"Original vector: {v}")
  plot_arrow(ax,w,"g",f"Vector on rotation: {w}")
  plt.xlim((-6,6))
  plt.ylim((-6,6))
  plt.grid(alpha=0.4)
  ax.set_aspect("equal")

Using the function to rotate [3.0 5.0] by 60 degrees anti-clockwise

plot_rot(np.pi/3,np.array([3.0,5.0]))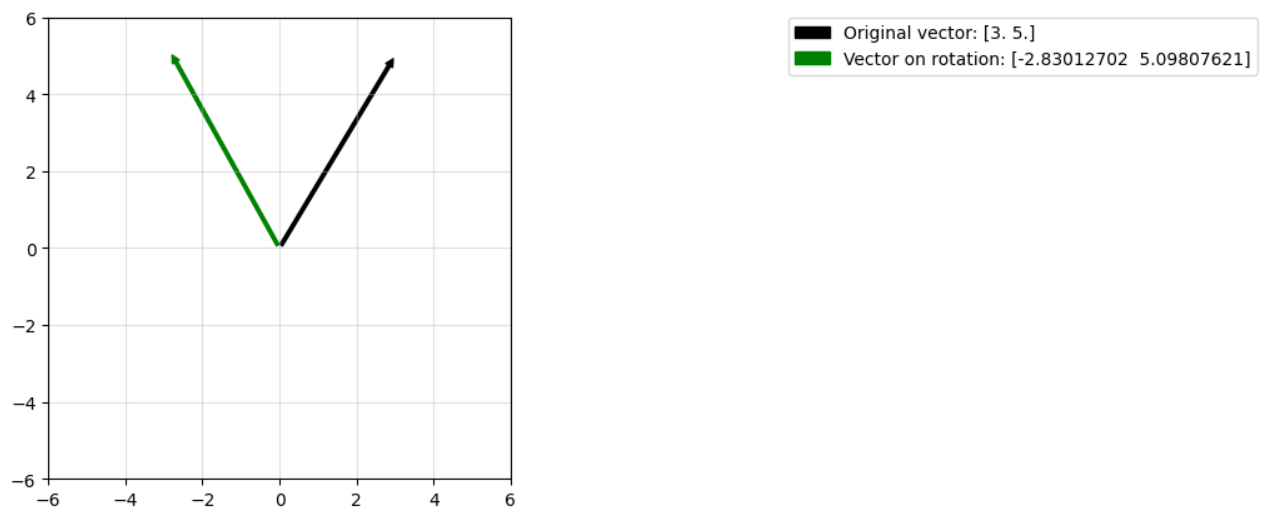

Matrix multiplication as transformation

Rank of a matrix is the minimum number of linearly independent rows and columns or the number of non-zero eigenvalues in case of a square matrix.

Consider the low rank matrix:

Defining the function:

def plot_lr(v,slope):
  A1 = np.array([1.0, 2.0])
  A = np.vstack((A1,slope*A1)) # The low rank matrix
  x = np.arange(-6,6,0.01)
  y = slope*x
  plot_transform(A,v)
  plt.plot(x,y,lw=5,alpha=0.4,label=f"y = {slope}x, Column Space of A")
  plt.legend(bbox_to_anchor=(1,1),borderaxespad=0)

Lets transform the vector [1.0 2.0] using the above transformation matrix:

plot_lr(np.array([1.0, 2.0]),4)
plt.tight_layout()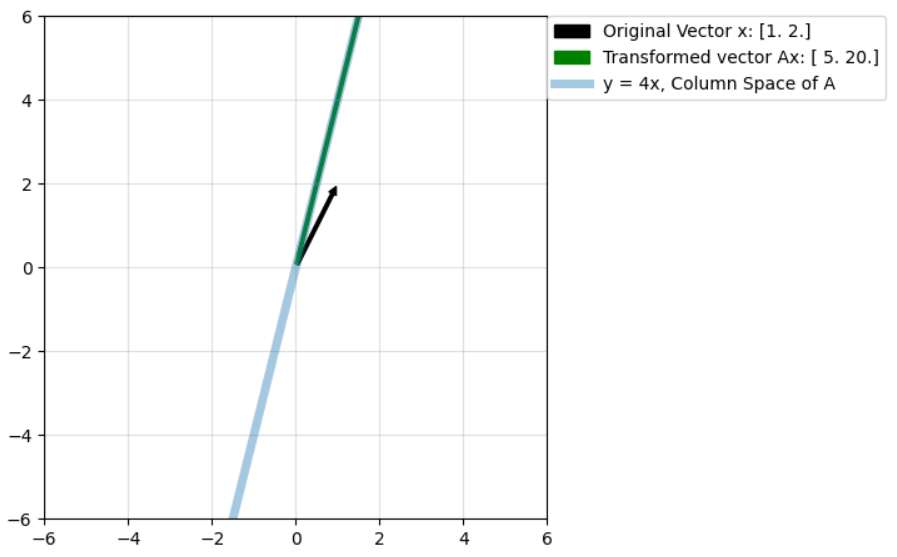

Importance of rowspace, columnspace and nullspace in low rank matrix transformations

A = np.array([[1.0,2.0],[4.0,8.0]])
print("The transformation matrix involved is :")
Matrix(A)

print("The rowspace of this matrix is spanned by : ")
Matrix(np.array([1.0,2.0]))

print("The nullspace of a matrix is always perpendicular to the rowspace.")
print("The nullspace of matrix A is spaned by : ")
Matrix(np.array([-2.0,1.0]))

print("Any vector in the nullspace is converted to a zero matrix after transformation.")
plot_lr(np.array([2.0,-1.0]),4)
plt.plot(x,-0.5*x,lw=5,alpha=0.4,label=f"y = {-0.5}x, Nullspace of A",color="g")
x = np.arange(-6,6,0.01)
plt.legend(bbox_to_anchor=(1,1), borderaxespad=0)
plt.tight_layout()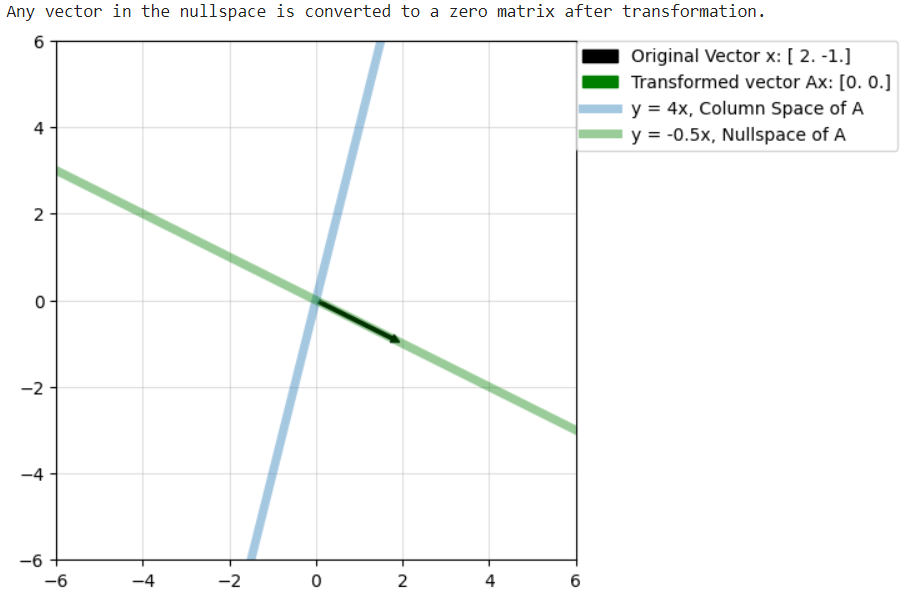

Consider the vector v = [1.0, 1.0] and the same low rank transformation matrix as above.

The matrix obtained on transformation is: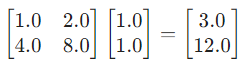

The projection of v along the rowspace of A is:

Step 1: Finding the projection matrix:

r = np.array([1.0, 2.0])
proj = np.outer(r,r)
proj = proj / np.inner(r,r)
Matrix(proj)

The projection matrix is:

Step 2: Finding the projection of v along the rowspace of A

b = np.array([1.0,1.0])
v = proj @ b
Matrix(v)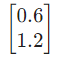

The matrix obtained on transformation of this projection vector is:

Av = A @ v
Eq(MatMul(Matrix(A),Matrix(v)),Matrix(Av),evaluate=False)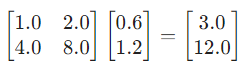

We notice that this is the same as the matrix obtained before.

Learnings:

  1. Any vector can be written as the vector sum of the projection on the rowspace and projection perpendicular to the rowspace (ie; in the nullspace). Only the component along the rowspace gets transformed to a non-zero matrix, the transformation of the component in the nullspace is always a zero matrix.

  2. Analogy to PCA: As all vectors after transformation lie in the column space of A, this can be thought of as dimensionality reduction where there is a change in dimension from the initial vector space to the dimension of the column space of the transformation matrix